
🤩 Approximation
근사에 대해서 알아보고, 파이썬을 통해서 간단한 예제 문제를 풀도록 하겠습니다.
파이썬 문제는 https://wikidocs.net/165632를 참고했습니다
문제
포아송 분포와 정규 분포를 이용해 이항 분포를 근사Approximate해보세요.
베이스라인의 code here 을 채우세요.
베이스라인
from scipy.stats import binom, poisson, norm
import matplotlib.pyplot as plt
def poisson_binom_plot(n, p):
lamb = # code here
mu = # code here
std = # code here
x_min = int(-n*0.2)
x_max = int(n*1.2)
probs_binom = [binom.pmf(i,n,p) for i in range(x_min, x_max+1)]
probs_poisson = # code here
probs_norm = # code here
plt.plot(range(x_min, x_max+1), probs_binom, alpha=0.5)
plt.plot(range(x_min, x_max+1), probs_poisson, alpha=0.5)
plt.plot(range(x_min, x_max+1), probs_norm, alpha=0.5)
plt.legend(['binom', 'poisson', 'norm'])
plt.title(f'N={n}, p={p}')
plt.show()
Input
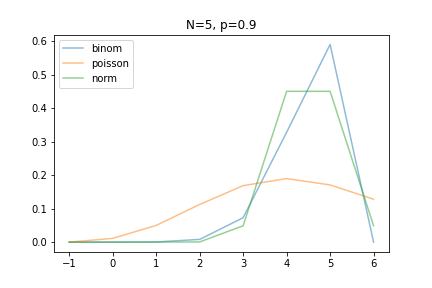
poisson_binom_plot(5, 0.9)
poisson_binom_plot(20, 0.4)
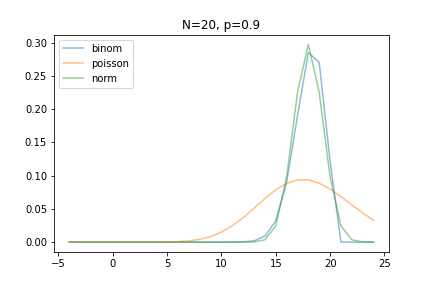
poisson_binom_plot(20, 0.9)
poisson_binom_plot(40, 0.9)
poisson_binom_plot(100, 0.0001)
Output



베이스 라인(정답 - 더보기 클릭)
더보기
from scipy.stats import binom, poisson, norm
import matplotlib.pyplot as plt
def poisson_binom_plot(n, p):
## lambda, mu는 binomial distribution, poisson distribution의 관계성에 의해서
## binomial의 평균과 분산은 np로 계산 하기 때문에 동일하게 np로 처리
lamb = n * p # 포아송 분포의 평균(lambda, 람다)값 계산
mu = n * p # 정규 분포의 평균(mu, 뮤)값
std = (n * p * ( 1 - p)) ** 0.5 # 정규 분포의 표준편차 값
## numpy를 사용하면 std = np.sqrt(n*p*(1-p))로 처리 가능 np.sqrt가 ** 0.5랑 동일한 작용
x_min = int(-n*0.2)
x_max = int(n*1.2)
probs_binom = [binom.pmf(i,n,p) for i in range(x_min, x_max+1)]
probs_poisson = # code here
probs_norm = # code here
plt.plot(range(x_min, x_max+1), probs_binom, alpha=0.5)
plt.plot(range(x_min, x_max+1), probs_poisson, alpha=0.5)
plt.plot(range(x_min, x_max+1), probs_norm, alpha=0.5)
plt.legend(['binom', 'poisson', 'norm'])
plt.title(f'N={n}, p={p}')
plt.show()
이항 분포, 포아송 분포, 정규 분포의 의미
이항 분포 (Binomial Distribution):
- 의미: 이항 분포는 주어진 횟수(n)의 독립적인 시행에서 각각의 시행이 성공할 확률(p)을 가질 때, 특정 횟수(k)만큼 성공할 확률을 나타내는 분포입니다.
- 예시: 동전 던지기에서 앞면이 나올 확률, 제품 검사에서 불량품이 나올 확률 등.
포아송 분포 (Poisson Distribution):
- 의미: 포아송 분포는 특정 시간 또는 공간 내에서 평균적으로 λ번 일어나는 사건이 k번 일어날 확률을 나타내는 분포입니다. 이항 분포에서 n이 매우 크고 p가 매우 작을 때 포아송 분포로 근사할 수 있습니다.
- 예시: 1시간 동안 걸려오는 전화 횟수, 단위 면적당 발생하는 교통사고 횟수 등.
정규 분포 (Normal Distribution):
- 의미: 정규 분포는 평균(μ)과 표준편차(σ)로 정의되는 연속적인 확률 분포로, 자연 현상이나 사회 현상에서 가장 흔하게 나타나는 분포입니다. 이항 분포에서 n이 충분히 크면 정규 분포로 근사할 수 있습니다.
- 예시: 사람들의 키, 몸무게, 시험 점수 등.
간단한 예시를 통해서 이항 분포, 포아송 분포, 정규 분포에 대해서 설명 드렸습니다. Input과 Output를 통해서 이항 분포를 포아송 분포와 정규 분포로 근사할 수 있음을 보여주는데, 입력되어지는 n과 p값에 따른 어떠한 분포가 이항분포와 더 잘 근사하는지에 대해서 비교 할 수 있습니다.
비교 :
- 이항 분포가 포아송 분포와 근사하는 경우에는 n이 크고 p가 작은 경우입니다.
- 이항 분포가 정규 분포와 근사하는 경우에는 n이 충분히 큰 경우입니다.
'공부 > 파이썬을 통한 기초통계학' 카테고리의 다른 글
| Expectation, 기댓값 (0) | 2025.03.07 |
|---|---|
| Negative binomial distribution, 음이항 분포 (0) | 2025.02.27 |
| Standardization(표준화), Normalization(정규화) (0) | 2025.02.24 |
| Poisson Distribution, 포아송 분포 (0) | 2025.02.20 |
| Binomial distribution, 이항 분포 (0) | 2025.02.19 |